Calculating the p-value for a chi-square test is an essential skill for anyone working with statistical data. The p-value is the probability that the observed results are due to chance alone. In other words, it is the probability of obtaining a test statistic as extreme or more extreme than the one observed, assuming the null hypothesis is true.

To calculate the p-value for a chi-square test, you need to know the degrees of freedom and the chi-square test statistic. The degrees of freedom depend on the number of categories in the data, while the chi-square test statistic measures the difference between the observed and expected frequencies. Once you have these values, you can use a chi-square distribution table or an online bankrate piti calculator to find the p-value.

Understanding how to calculate the p-value for a chi-square test is critical in many fields, including biology, psychology, and economics. It allows researchers to determine whether the results of their experiments are statistically significant and whether they should reject or accept the null hypothesis. By mastering this skill, researchers can draw more accurate conclusions from their data and make more informed decisions based on their findings.

Understanding Chi-Square Tests

Definition and Purpose

Chi-square tests are statistical tests used to determine whether there is a significant association between two categorical variables. It is a non-parametric test, meaning that it does not make any assumptions about the distribution of the data. Instead, it compares the observed data to what would be expected under a null hypothesis of no association.

The test is based on the chi-square statistic, which measures the difference between the observed and expected frequencies. The larger the difference, the larger the chi-square value and the more evidence there is against the null hypothesis.

Chi-square tests can be used to analyze data from a wide range of fields, including biology, psychology, marketing, and more. They are often used in surveys and experiments to determine whether there is a relationship between two variables.

Types of Chi-Square Tests

There are two main types of chi-square tests: the goodness-of-fit test and the test of independence.

The goodness-of-fit test is used to determine whether the observed data fits a particular distribution. For example, it can be used to determine whether the observed data follows a normal distribution.

The test of independence is used to determine whether there is a significant association between two categorical variables. For example, it can be used to determine whether there is a significant association between gender and political affiliation.

Chi-square tests can be performed using software such as Microsoft Excel or statistical software such as SPSS. However, it is important to understand the underlying principles of the test and how to interpret the results.

The P Value Concept

Definition of P Value

The p-value is a statistical measure that helps determine the significance of results in a hypothesis test. It represents the probability of obtaining a result as extreme or more extreme than the observed result, assuming the null hypothesis is true. In other words, it measures the strength of evidence against the null hypothesis.

A p-value is a number between 0 and 1. A small p-value (e.g., less than 0.05) indicates strong evidence against the null hypothesis, while a large p-value (e.g., greater than 0.05) indicates weak evidence against the null hypothesis.

Significance Levels

Significance levels are pre-determined thresholds used to interpret p-values. The most commonly used significance level is 0.05, which means that if the p-value is less than 0.05, the result is considered statistically significant.

However, it is important to note that significance levels are arbitrary and should be chosen based on the context of the study. A lower significance level (e.g., 0.01) may be appropriate for studies where false positives are particularly problematic, while a higher significance level (e.g., 0.10) may be appropriate for exploratory studies.

In summary, the p-value is a measure of the strength of evidence against the null hypothesis, and significance levels are used to interpret p-values. It is important to choose an appropriate significance level based on the context of the study.

Chi-Square Test Assumptions

The chi-square test is a statistical test that is used to determine whether there is a significant association between two categorical variables. However, before conducting the test, there are several assumptions that must be met. In this section, we will discuss the sample size requirements, expected frequencies, and independence of observations assumptions.

Sample Size Requirements

One of the assumptions of the chi-square test is that the sample size should be large enough. The general rule of thumb is that each cell in the contingency table should have an expected frequency of at least 5. If this assumption is not met, the chi-square test may not be reliable.

Expected Frequencies

Another assumption of the chi-square test is that the expected frequencies should be greater than 1. If any of the expected frequencies are less than 1, the chi-square test may not be reliable. In this case, Fisher's exact test or another appropriate test should be used.

Independence of Observations

The final assumption of the chi-square test is that the observations should be independent. This means that each participant should only be counted once and that the observations should not be influenced by each other. If the observations are not independent, the chi-square test may not be reliable.

In summary, before conducting a chi-square test, it is important to ensure that the sample size requirements, expected frequencies, and independence of observations assumptions are met. By doing so, researchers can ensure that the results of the test are reliable and accurate.

Calculating P Value for Chi-Square

Chi-square is a statistical test used to determine whether an observed set of categorical data differs significantly from the expected set of data. The p value for a chi-square test indicates the probability of obtaining the observed data or more extreme results if the null hypothesis is true.

Observed vs. Expected Frequencies

To calculate the p value for a chi-square test, one must first calculate the expected frequencies. The expected frequencies are the frequencies that would be expected if the null hypothesis were true. The observed frequencies are the frequencies that were actually observed in the data.

Chi-Square Test Statistic Formula

Once the observed and expected frequencies are calculated, the chi-square test statistic can be calculated using the following formula:

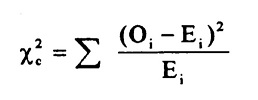
where O is the observed frequency, E is the expected frequency, and k is the number of categories.

Degrees of Freedom

The degrees of freedom for a chi-square test are calculated as (k-1), where k is the number of categories. Degrees of freedom represent the number of values in the final calculation that are free to vary.

Using Chi-Square Distribution Tables

Chi-square distribution tables can be used to find the p value associated with a particular chi-square test statistic and degrees of freedom. The p value is the area under the chi-square distribution curve to the right of the calculated chi-square test statistic.

Software and Calculators

There are various software and online calculators available to calculate the p value for a chi-square test. These tools can save time and reduce the risk of errors in calculations. However, it is important to understand the underlying concepts and formulas to ensure accurate interpretation of the results.

Interpreting the Results

Analyzing the P Value

After calculating the chi-square test and obtaining the p-value, the next step is to interpret the results. The p-value is a critical component in statistical hypothesis testing, representing the probability that the observed data would occur if the null hypothesis were true. A small p-value indicates that the observed data is unlikely to have occurred by chance, and provides evidence against the null hypothesis.

Typically, a significance level of 0.05 is used to determine whether the null hypothesis should be rejected or not. If the p-value is less than 0.05, the null hypothesis is rejected, and the alternative hypothesis is accepted. On the other hand, if the p-value is greater than 0.05, the null hypothesis is not rejected, and there is insufficient evidence to support the alternative hypothesis.

Contextualizing with Research Hypotheses

When interpreting the results of the chi-square test, it is important to contextualize the findings with the research hypotheses. The null hypothesis represents the absence of a relationship between two categorical variables, while the alternative hypothesis represents the presence of a relationship.

For example, suppose a researcher is interested in studying the relationship between gender and political affiliation. The null hypothesis would be that there is no relationship between gender and political affiliation, while the alternative hypothesis would be that there is a relationship.

If the chi-square test results in a small p-value, the researcher can conclude that there is evidence to support the alternative hypothesis, and that there is a relationship between gender and political affiliation. On the other hand, if the chi-square test results in a large p-value, the researcher cannot conclude that there is a relationship between gender and political affiliation, and the null hypothesis cannot be rejected.

In summary, interpreting the results of the chi-square test involves analyzing the p-value and contextualizing the findings with the research hypotheses. The p-value provides evidence for or against the null hypothesis, while the research hypotheses provide the context for understanding the relationship between the categorical variables being studied.

Reporting the Findings

Presenting the Chi-Square Results

After calculating the chi-square test and determining the p value, the next step is to present the findings. When reporting the results of a chi-square test, it is important to include the degrees of freedom, typically denoted as "df". The degrees of freedom refer to the number of categories that can vary freely in the calculation of a statistic. In a chi-square test, the degrees of freedom are equal to the number of categories minus one.

It is also important to indicate the chi-square statistic value and the p value. The chi-square statistic value represents the difference between the observed and expected frequencies, while the p value represents the probability that the observed data would occur if the null hypothesis were true. The p value is a critical component in statistical hypothesis testing and is typically set at a significance level of 0.05.

One way to present the chi-square results is to use a table. The table should include the observed and expected frequencies for each category, as well as the chi-square statistic value and the p value. It is also helpful to include the degrees of freedom and the sample size.

Discussing Implications of the P Value

Once the chi-square results have been presented, it is important to discuss the implications of the p value. A p value of less than 0.05 indicates that the null hypothesis can be rejected, and there is evidence to support the alternative hypothesis. On the other hand, a p value greater than 0.05 indicates that the null hypothesis cannot be rejected, and there is insufficient evidence to support the alternative hypothesis.

When discussing the implications of the p value, it is important to consider the context of the study and the research question. A statistically significant result may have practical or theoretical implications, but it is also important to consider the effect size and the magnitude of the difference between the observed and expected frequencies.

In summary, reporting the findings of a chi-square test involves presenting the degrees of freedom, the chi-square statistic value, and the p value. It is also important to discuss the implications of the p value in the context of the study and the research question. By following these guidelines, researchers can accurately and effectively report the results of their chi-square analysis.

Frequently Asked Questions

How can I calculate the p-value from a chi-square statistic by hand?

To calculate the p-value from a chi-square statistic by hand, you will need to use a chi-square distribution table. Once you have calculated the chi-square statistic, you can use the degrees of freedom and the critical value to look up the p-value on the table. The process for finding the p-value using a table can be time-consuming and error-prone, so it is often easier to use a calculator or statistical software.

What is the process for finding the p-value from a chi-square statistic using a TI-84 calculator?

To find the p-value from a chi-square statistic using a TI-84 calculator, you will need to use the chi-square cumulative distribution function (CDF). First, calculate the chi-square statistic and degrees of freedom. Then, use the CDF function to find the cumulative probability for the chi-square statistic. Subtract the cumulative probability from 1 to find the p-value.

How can I interpret the p-value in the context of a chi-square test?

The p-value is a measure of the evidence against the null hypothesis in a chi-square test. A small p-value (typically less than 0.05) indicates that the observed data is unlikely to have occurred by chance alone, and provides evidence in favor of the alternative hypothesis. A large p-value suggests that there is not enough evidence to reject the null hypothesis.

What steps are involved in using Excel to calculate the p-value from a chi-square test?

To calculate the p-value from a chi-square test using Excel, you will first need to calculate the chi-square statistic and degrees of freedom. Then, use the CHISQ.DIST.RT function to find the right-tailed p-value. The function takes the chi-square statistic and degrees of freedom as inputs.

How do you determine the p-value from a chi-square statistic and its associated degrees of freedom?

To determine the p-value from a chi-square statistic and its associated degrees of freedom, you will need to use a chi-square distribution table or a calculator. The p-value is the area to the right of the chi-square statistic on the chi-square distribution, with degrees of freedom equal to the associated degrees of freedom.

What method is used to calculate the p-value from a frequency table using the chi-square test?

To calculate the p-value from a frequency table using the chi-square test, you will first need to calculate the expected frequencies for each cell in the table. Then, use the chi-square formula to calculate the chi-square statistic. Finally, use the degrees of freedom and the chi-square distribution to determine the p-value.