How to Calculate Expected Frequency: A Clear Guide
Expected frequency is a statistical concept used to calculate the number of times an event is expected to occur based on probability. It is used in various fields, including medicine, social sciences, and economics, to analyze data and make predictions. Expected frequency is an important concept in hypothesis testing, which is used to determine whether a particular hypothesis is true or false.
To calculate expected frequency, one must first determine the probability of each event occurring. This can be done by dividing the number of times the event occurred by the total number of events. Once the probabilities are determined, the expected frequency can be calculated by multiplying the probability of each event by the total number of events. This will give the number of times each event is expected to occur.
Expected frequency is often used in contingency tables, which are used to analyze data that has been divided into categories. In these tables, the expected frequency is compared to the observed frequency, which is the actual number of times an event occurred. The difference between the expected and observed frequencies is used to determine whether there is a significant relationship between the variables being analyzed.
Fundamentals of Probability Theory
Probability theory is the branch of mathematics that deals with the study of random phenomena. It is a fundamental concept in statistics, data analysis, and machine learning. Probability theory is used to model and analyze uncertain events and to quantify the likelihood of different outcomes.
The basic idea of probability theory is that we can assign a probability to each possible outcome of an event. The probability of an event is a number between 0 and 1, where 0 represents an impossible event and 1 represents a certain event. For example, the probability of rolling a 6 on a fair six-sided die is 1/6.
Probability theory has two main branches: discrete probability and continuous probability. Discrete probability deals with events that have a finite number of possible outcomes, such as rolling a die or flipping a coin. Continuous probability deals with events that have an infinite number of possible outcomes, such as the height of a person or the temperature of a room.
The fundamental concepts of probability theory include events, sample spaces, outcomes, probability distributions, and expected values. A sample space is the set of all possible outcomes of an event. An event is a subset of the sample space. An outcome is a particular result of an event. A probability distribution is a function that assigns probabilities to each possible outcome of an event. The expected value is the average value of a random variable over many trials.
In summary, probability theory is a fundamental concept in statistics and data analysis. It provides a framework for modeling and analyzing uncertain events and quantifying the likelihood of different outcomes. The basic concepts of probability theory include events, sample spaces, outcomes, probability distributions, and expected values.
Concept of Expected Frequency
Expected frequency is a statistical concept used to calculate the number of times an event is expected to occur in a given set of data. It is a theoretical value that represents the average mortgage payment massachusetts (d1.therpsite.com) number of times an event is likely to occur if the data is repeated many times.
Expected frequency is calculated using probability theory and contingency tables. A contingency table is a table that displays the frequencies of two or more variables in a data set. It is used to determine whether there is a relationship between the variables.
To calculate the expected frequency of each cell in a contingency table, the row and column totals are multiplied and divided by the total number of observations in the table. The formula for expected frequency is:
Expected frequency = (row total * column total) / table total
For example, if a contingency table has 2 rows and 2 columns, then there are 4 cells. The expected frequency for each cell is calculated by multiplying the row total and column total for that cell and dividing the result by the table total.
Expected frequency is an important concept in statistics because it enables researchers to compare the observed frequencies in a data set with the frequencies that are expected to occur by chance. This can help researchers determine whether there is a significant relationship between variables in the data set.
In summary, expected frequency is a theoretical value that represents the average number of times an event is likely to occur if the data is repeated many times. It is calculated using probability theory and contingency tables and is an important concept in statistics for determining whether there is a significant relationship between variables in a data set.
Calculating Expected Frequency
Expected frequency is a statistical term that refers to the number of times an event is expected to occur in a given sample or population. It is an important concept in statistics because it allows researchers to test hypotheses and make predictions about the likelihood of different outcomes.
Defining the Hypothesis
Before calculating expected frequency, researchers must first define their hypothesis. A hypothesis is an educated guess about the relationship between two or more variables. For example, a researcher might hypothesize that there is a relationship between a person's age and their likelihood of developing a certain disease.
Identifying Relevant Variables
Once the hypothesis has been defined, researchers must identify the relevant variables. Variables are factors that can affect the outcome of the study. In the example above, the relevant variables would be age and disease.
Determining Probability Distributions
Finally, researchers must determine the probability distributions of the variables. Probability distributions describe the likelihood of different outcomes. For example, if a researcher wants to determine the expected frequency of a certain disease among people of a certain age, they would need to know the probability distribution of the disease and the probability distribution of age.
To calculate expected frequency, researchers can use a formula that takes into account the probability distributions of the relevant variables. This formula is (row sum * column sum) / table sum. Researchers can repeat this formula to obtain the expected value for each cell in the table.
Overall, calculating expected frequency is an important tool for researchers who want to make predictions about the likelihood of different outcomes. By defining their hypothesis, identifying relevant variables, and determining probability distributions, researchers can use expected frequency to test their hypotheses and make informed decisions.
Expected Frequency in Genetics
Punnett Squares
Punnett Squares are a simple and useful tool for predicting the expected frequency of genotypes in offspring from two parents. A Punnett Square is a grid that shows all possible combinations of alleles from the parents and their probability of occurring. By multiplying the probabilities of each possible combination, the expected frequency of each genotype can be calculated.
For example, if a homozygous dominant parent (AA) is crossed with a homozygous recessive parent (aa), the Punnett Square would show that all offspring will be heterozygous (Aa) with an expected frequency of 100%.
Hardy-Weinberg Principle
The Hardy-Weinberg Principle is a mathematical formula used to calculate the expected frequency of alleles and genotypes in a population. The principle assumes that the population is large, randomly mating, and not subject to any evolutionary forces such as mutation, migration, or natural selection.
The equation for the Hardy-Weinberg Principle is p^2 + 2pq + q^2 = 1, where p is the frequency of the dominant allele, q is the frequency of the recessive allele, p^2 is the frequency of the homozygous dominant genotype, q^2 is the frequency of the homozygous recessive genotype, and 2pq is the frequency of the heterozygous genotype.
Using the Hardy-Weinberg Principle, the expected frequency of genotypes can be calculated from the allele frequencies in a population. This principle is particularly useful for studying the genetic structure of populations and detecting deviations from expected frequencies that may indicate evolutionary forces at work.
In summary, Punnett Squares and the Hardy-Weinberg Principle are both useful tools for calculating the expected frequency of genotypes in genetics. Punnett Squares are used to predict the offspring of a single cross between two parents, while the Hardy-Weinberg Principle is used to calculate the expected frequency of genotypes in a population.
Expected Frequency in Contingency Tables
When analyzing the relationship between two categorical variables, a contingency table is used to display the frequencies for all possible combinations of the variables. Expected frequency is a measure that helps to determine if the observed frequencies in a contingency table are significantly different from the expected frequencies.
Chi-Square Test
One way to determine if the observed frequencies are significantly different from the expected frequencies is by using the chi-square test. The chi-square test is a statistical test that compares the observed frequencies to the expected frequencies in a contingency table to determine if there is a significant association between the two variables.
The formula for calculating the chi-square test statistic is:
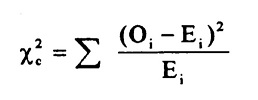
where O represents the observed frequency, E represents the expected frequency, and the sum is taken over all cells in the contingency table.
If the calculated chi-square test statistic is greater than the critical value from the chi-square distribution with degrees of freedom equal to (number of rows - 1) x (number of columns - 1) at a chosen level of significance, then there is evidence to reject the null hypothesis that there is no association between the two variables.
Degrees of Freedom
The degrees of freedom for a contingency table is equal to (number of rows - 1) x (number of columns - 1). The degrees of freedom is used to determine the critical value from the chi-square distribution for a given level of significance.
In general, a higher degrees of freedom indicates that there is a larger number of cells in the contingency table, which increases the complexity of the analysis. However, it also increases the power of the chi-square test to detect significant associations between the variables.
Overall, expected frequency is an important measure in contingency tables that helps to determine if the observed frequencies are significantly different from the expected frequencies. The chi-square test is a common statistical test that can be used to analyze the association between two categorical variables in a contingency table.
Applications in Real-World Scenarios
Market Research
Expected frequency is a useful tool in market research to determine the likelihood of certain outcomes. For example, a company may conduct a survey to determine the likelihood of consumers purchasing a new product. By calculating the expected frequency, the company can estimate the number of potential customers and make informed decisions about the product's launch.
Market researchers can also use expected frequency to analyze survey data and identify patterns. For instance, they can determine if there is a relationship between two variables, such as age and product preference, by using the chi-square test of independence. This analysis can help identify target demographics and inform marketing strategies.
Quality Control
Expected frequency is also used in quality control to ensure that products meet certain standards. For example, a manufacturer may use expected frequency to monitor the number of defective products in a batch. By calculating the expected frequency of defects, the manufacturer can determine if the number of defects is within an acceptable range.
Quality control professionals can also use expected frequency to identify trends and patterns in data. For instance, they can use the chi-square goodness of fit test to determine if a sample of products meets a certain specification. This analysis can help identify areas for improvement in the manufacturing process.
Overall, expected frequency is a valuable tool in many real-world scenarios, from market research to quality control. By using this statistical method, professionals can make informed decisions and improve their processes.
Statistical Significance and Error Analysis
After calculating the expected frequency, the next step is to determine whether the results are statistically significant. Statistical significance is a measure of whether the observed differences between groups are due to chance or not. In other words, it tells us whether the results are likely to be real or just a coincidence.
One way to determine statistical significance is to conduct a chi-square test. The chi-square test compares the observed frequencies to the expected frequencies and calculates a p-value. The p-value is the probability of obtaining results as extreme or more extreme than the observed results, assuming that the null hypothesis is true. If the p-value is less than the significance level (usually 0.05), then the results are considered statistically significant.
It is important to note that statistical significance does not necessarily mean practical significance. Practical significance refers to the magnitude of the observed differences and whether they are meaningful in real-world terms. For example, a study may find a statistically significant difference in the effectiveness of two treatments, but the difference may be so small that it is not clinically meaningful.
Another consideration when interpreting results is error analysis. Error analysis is the process of identifying and quantifying sources of error in the study design or data collection. Common sources of error include sampling bias, measurement error, and confounding variables. By identifying and addressing sources of error, researchers can increase the validity and reliability of their results.
In summary, calculating expected frequency is an important step in statistical analysis, but it is not the only consideration. Statistical significance and error analysis are also important factors to consider when interpreting results. By understanding these concepts, researchers can draw more accurate and meaningful conclusions from their data.
Limitations of Expected Frequency Analysis
While expected frequency analysis can be a useful tool for analyzing data, it is important to be aware of its limitations.
One limitation is that expected frequency analysis assumes that the data follows a certain distribution. If the data does not follow this distribution, then the results of the analysis may not be accurate.
Another limitation is that expected frequency analysis assumes that the sample size is large enough. If the sample size is too small, then the results of the analysis may not be accurate.
Additionally, expected frequency analysis assumes that the variables being analyzed are independent. If the variables are not independent, then the results of the analysis may not be accurate.
It is also important to note that expected frequency analysis does not take into account any confounding variables that may be present in the data. Confounding variables can have a significant impact on the results of an analysis, and failing to account for them can lead to inaccurate conclusions.
Overall, while expected frequency analysis can be a useful tool for analyzing data, it is important to be aware of its limitations and to use it in conjunction with other analytical tools to ensure accurate results.
Frequently Asked Questions
How can expected frequency be determined in a chi-square test?
Expected frequency can be determined in a chi-square test by using the formula: expected frequency = (row total x column total) / grand total. This formula can be used to calculate the expected frequency for each cell in a contingency table. The chi-square test is used to determine whether there is a significant association between two categorical variables.
What is the process for deriving expected frequency from observed frequency data?
The process for deriving expected frequency from observed frequency data involves calculating the expected frequency for each cell in a contingency table using the formula: expected frequency = (row total x column total) / grand total. The observed frequency data is then compared to the expected frequency data using a statistical test, such as the chi-square test, to determine whether there is a significant association between two categorical variables.
What steps are involved in calculating expected frequency using Microsoft Excel?
To calculate expected frequency using Microsoft Excel, you can use the formula: expected frequency = (row total x column total) / grand total. You can enter the observed frequency data into a contingency table in Excel and then use the formula to calculate the expected frequency for each cell. Excel also has built-in functions, such as CHISQ.TEST, that can be used to perform statistical tests on the observed and expected frequency data.
How is expected frequency computed in a goodness of fit test?
In a goodness of fit test, expected frequency is computed by using the formula: expected frequency = (sample size x probability). This formula can be used to calculate the expected frequency for each category in a frequency distribution. The goodness of fit test is used to determine whether an observed frequency distribution fits a theoretical distribution.
What method is used to find expected frequency within a normal distribution?
In a normal distribution, the expected frequency can be found using the formula: expected frequency = (sample size x probability density function). The probability density function is used to describe the distribution of a continuous random variable. The expected frequency is used to determine the probability of observing a certain number of events within a normal distribution.
How can expected frequency be calculated in the context of a binomial distribution?
In a binomial distribution, the expected frequency can be calculated using the formula: expected frequency = (sample size x probability of success). This formula can be used to calculate the expected frequency for each possible outcome in a binomial experiment. The binomial distribution is used to model the number of successes in a fixed number of independent trials.
